推论1：三个角都相等的三角形是等边三角形 　　

英文：equilateral triangle，“等边三角形”也被称为“正三角形”。 　　

理解等边三角形的性质与判定

1.三边长度相等 　　
等边三角形的每条边上的中线、高或对角平分线重合。（三线合一）判定等边三角形等边三角形的复数性质 　　
内角的大小 60°

∴得高为√3/2 　　等边三角形的面积公式：设等边三角形的边长为x，那么面积S为4分之根号3，再乘以x平方。[1]

角和边的数量 3

　　

等边三角形（又称正三角形），为三边相等的三角形。其三个内角，均为60°。它是锐角三角形的一种。

性质编辑本段

等三线合一边三角形的内角都相等，且为60度 　　

2.三角度数为60度

其次明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形，等腰三角形不一定是等边三角形。

等边三角形的高和长的比√3比2 　　
∵设边为单位1，则底边为单位1/2，根据勾股定理（A的2次方+B的2次方=C 的2 次方）

2、等边三角形每条边上的中线、高线和所对角的平分线互相（三线合一） 　　

4、等边三角形的重要数据空间对称群

（2）三个内角都相等的三角形是等边　　

（3）有一个角是60度的等腰三角形是等边三角形 　　
等价于 A+wB+w^2C=0 　　其中 　　w=cos(2π/3)+isin(2π/3) 　　1+w+w^2=0 　　

（1）三边相等的三角形是等边三角形（定义） 　　

3、等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线或对角的平分线所在直线 。

等边三角形的高和长的关系 　　

首先明确等边三角形定义。三边相等的三角形叫做等边三角形，也称正三角形。 　　
推论2：有一个角等于60°的等腰三角形是等边三角形 　　等边三角形重心、内心 、外心、垂心重合于一点，称为等边三角形的中心。（四心合一） 　　
正三角形

判定 编辑本段

（首先考虑判断三角形是等腰三角形） 　　

A，bt网页游戏sf，B，C三点的复数构成正三角形 　　
二面体群 (D3)

满足其中任意一条即满足另一条，即为正三角形（又名等边三角形）： 　　
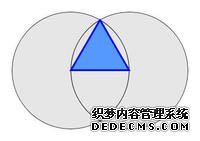
正三角形

正三角形

做正三角形编辑本段

可以利用尺规作图的方式画出正三角形，其作法相当简单： 先用尺画出一条任意长度的线段，等边三角形作法再分别以线段二端点为、线段为半径画圆，二圆汇交于二点，任选一点，和原来线段的两个端点画线，则这二条线和原来线段即构成一正三角形。

施莱夫利符号 {3}